[Data Structure] 트리(Tree)

8 분 소요

1. 트리

- 트리 (Tree) 구조

Node와 Branch를 이용해서, 사이클을 이루지 않도록 구성한 데이터 구조
트리 중 Binary Tree 형태의 구조로, 탐색(검색) 알고리즘 구현을 위해 많이 사용

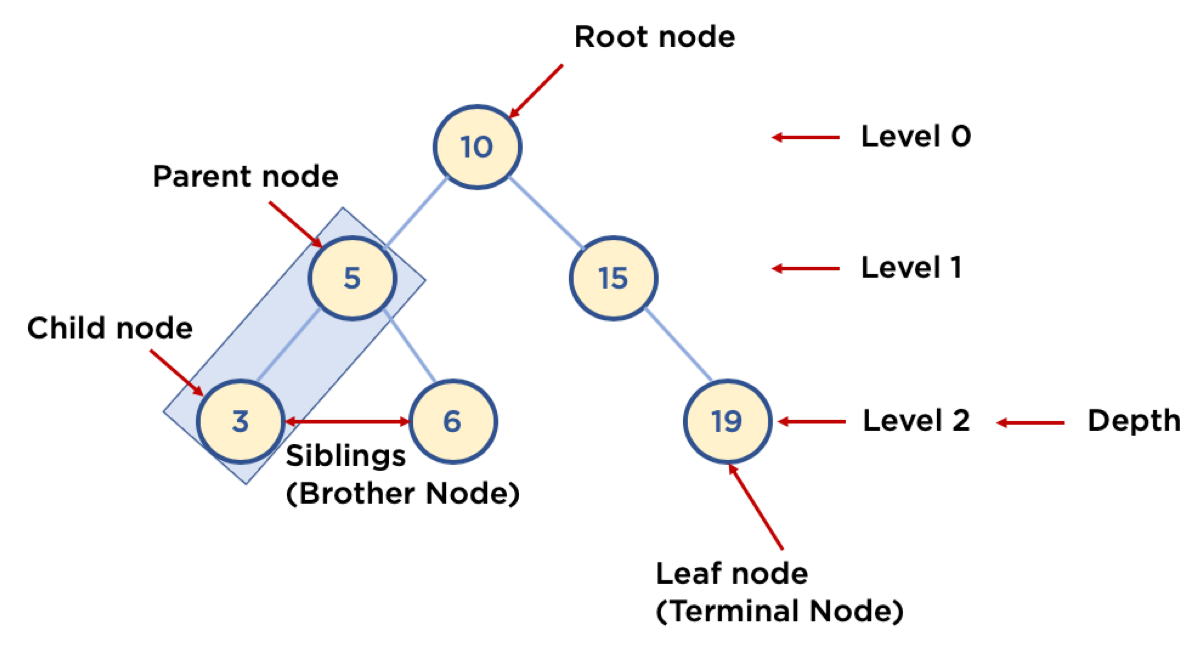
- 알아둘 용어

Node : 트리에서 데이터를 저장하는 기본 요소 (데이터와 다른 연결된 노드에 대한 Branch 정보 포함)
Root Node : 트리 맨 위에 있는 노드
Level : 최상위 노드를 Level 0으로 하였을 때, 하위 Branch로 연결된 노드의 깊이
Parent Node : 어떤 노드의 다음 레벨에 연결된 노드
Child Node : 어떤 노드의 상위 레벨에 연결된 노드
Leaf Node (Terminal Node) : Child Node가 하나도 없는 노드
Sibling (Brother Node) : 동일한 Parent Node를 가진 노드
Depth : 트리에서 Node가 가질 수 있는 최대 Level

- 이진 트리와 이진 탐색 트리

이진 트리 : 노드의 최대 Branch가 2인 트리
이진 탐색 트리 (Binary Search Tree, BST) : 이진 트리에 다음과 같은 추가적인 조건이 있는 트리
- 왼쪽 노드는 해당 노드보다 작은 값, 오른쪽 노드는 해당 노드보다 큰 값을 가짐

(출처: https://www.mathwarehouse.com/programming/gifs/binary-search-tree.php#binary-search-tree-insertion-node)

- 자료 구조 이진 탐색 트리의 장점과 주요 용도

주요 용도 : 데이터 검색(탐색)
장점 : 탐색 속도를 개선할 수 있음

- 이진트리와 정렬된 배열간의 탐색 비교

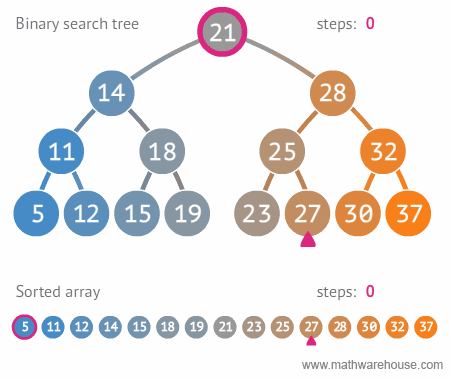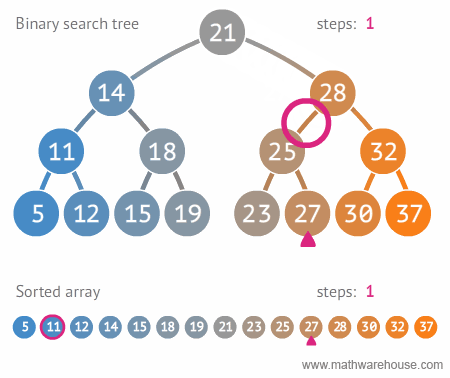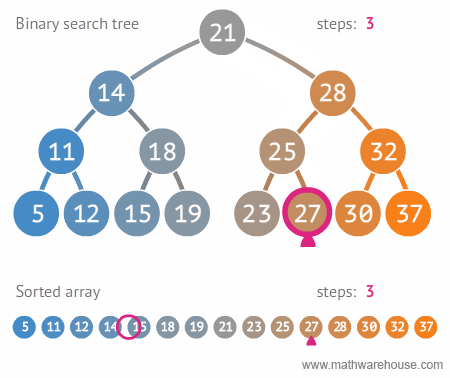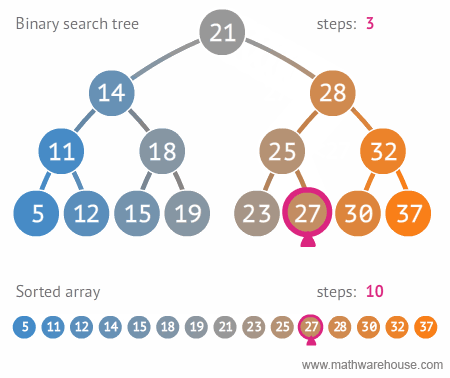
(출처: https://www.mathwarehouse.com/programming/gifs/binary-search-tree.php#binary-search-tree-insertion-node)

- 파이썬으로 이진 탐색 트리 구현하기

@1. 노드 클래스 만들기

class Node :
  def __init__(self, value) :
    self.value = value
    self.left = None
    self.right = None

@2. 이진 탐색 트리에 데이터 넣기

이진 탐색 트리 조건에 부합하게 데이터를 넣어야 함

class NodeMgmt :
  def __init__(self, head) :
    self.head = head

  def insert(self, value) :
    self.current_node = self.head
    while True :
      if value < self.current_node.value :
        if self.current_node.left != None :
          self.current_node = self.current_node.left
        else :
          self.current_node.left = Node(value)
          break
      else :
        if self.current_node.right != None :
          self.current_node = self.current_node.right
        else :
          self.current_node.right = Node(value)
          break


# 데이터 넣기
head = Node(1)
BST = NodeMgmt(head)
BST.insert(2)

@3. 이진 탐색 트리 탐색

class NodeMgmt :
  def __init__(self, value) :
    self.head = head

  def insert(self, value) :
    self.current_node = self.head
    while True :
      if value < self.current_node.value :
        if self.current_node.left != None :
          self.current_node = self.current_node.left
        else :
          self.current_node.left = Node(value)
          break
      else :
        if self.current_node.right != None :
          self.current_node = self.current_node.right
        else :
          self.current_node.right = Node(value)
          break

  def search(self, value) :
    self.current_node = self.head
    while self.current_node :
      if self.current_node.value == value :
        return True
      elif value < self.current_node.value :
        self.current_node = self.current_node.left
      else :
        self.current_node = self.current_node.right
    return False


# 데이터 삽입
head = Node(1)
BST = NodeMgmt(head)
BST.insert(2)
BST.insert(3)
BST.insert(0)
BST.insert(4)
BST.insert(8)

# 데이터 검색
BST.search(2)  # True
BST.search(-1)  # False

@4. 이진 탐색 트리 삭제

경우를 나누어서 이해
Leaf Node 삭제
- Leaf Node: Child Node 가 없는 Node
- 삭제할 Node의 Parent Node가 삭제할 Node를 가리키지 않도록 함

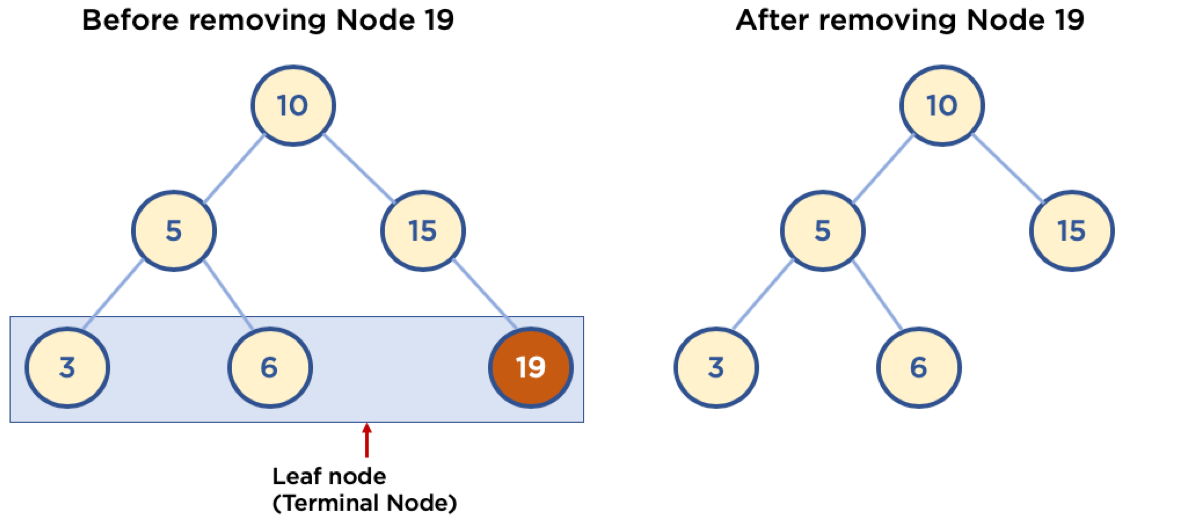
Child Node 가 하나인 Node 삭제
- 삭제할 Node의 Parent Node가 삭제할 Node의 Child Node를 가리키도록 함

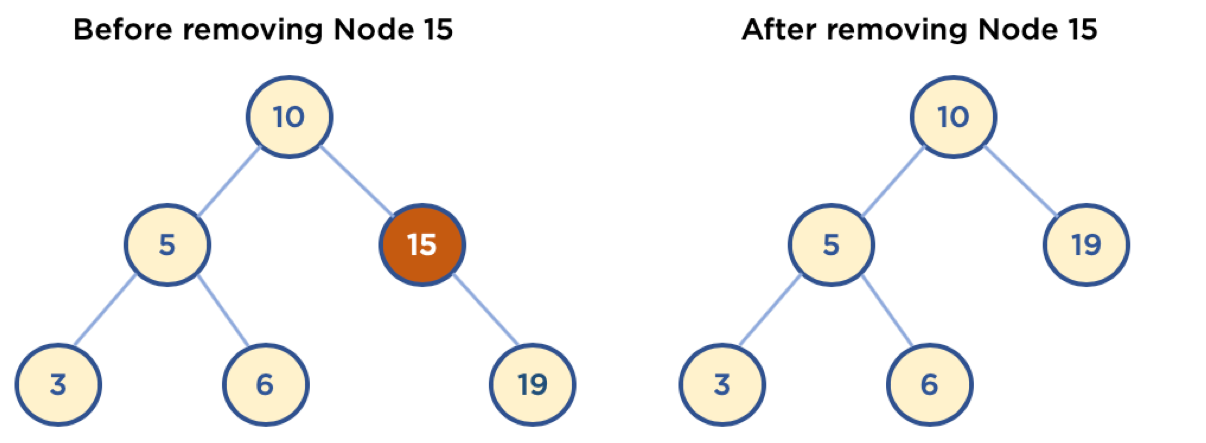
Child Node 가 두 개인 Node 삭제
1. 삭제할 Node의 오른쪽 자식 중, 가장 작은 값을 삭제할 Node의 Parent Node가 가리키도록 함
  - 삭제할 Node의 오른쪽 자식 선택
  - 오른쪽 자식의 가장 왼쪽에 있는 Node를 선택
  - 해당 Node를 삭제할 Node의 Parent Node의 왼쪽 Branch가 가리키게 함
  - 해당 Node의 왼쪽 Branch가 삭제할 Node의 왼쪽 Child Node를 가리키게 함
  - 해당 Node의 오른쪽 Branch가 삭제할 Node의 오른쪽 Child Node를 가리키게 함
  - 만약 해당 Node가 오른쪽 Child Node를 가지고 있었을 경우에는, 해당 Node의 본래 Parent Node의 왼쪽 Branch가 해당 오른쪽 Child Node를 가리키게 함
2. 삭제할 Node의 왼쪽 자식 중, 가장 큰 값을 삭제할 Node의 Parent Node가 가리키도록 함

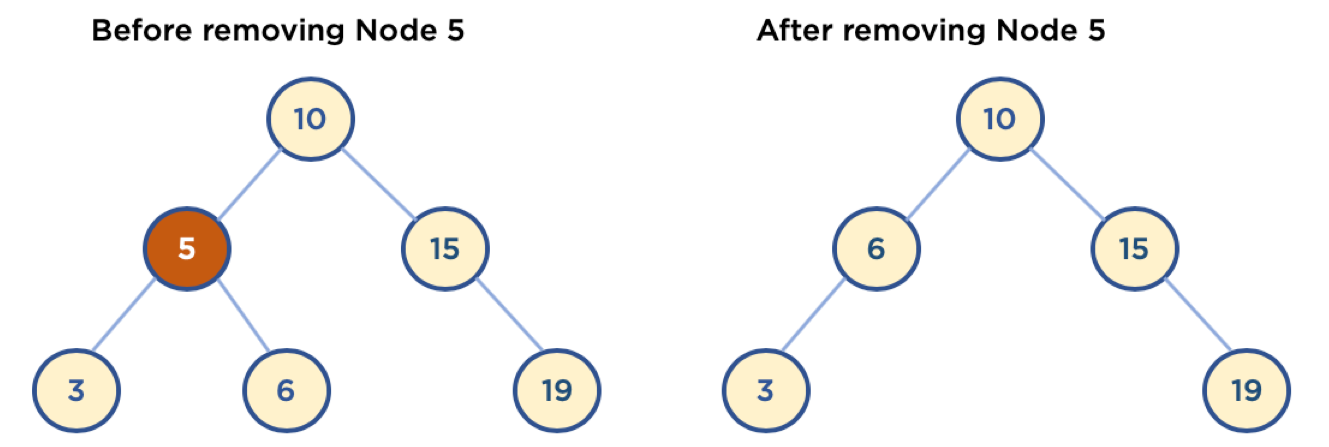
@5. 이진 탐색 트리 삭제 코드 구현과 분석

삭제할 Node 탐색
삭제할 Node가 없는 경우도 처리해야 함
이를 위해 삭제할 Node가 없는 경우는 False를 리턴하고, 함수를 종료 시킴

def delete(self, value) :
    searched = False
    self.current_node = self.head
    self.parent = self.head
    while self.current_node :
        if self.current_node.value == value :
            searched = True
            break
        elif value < self.current_node.value :
            self.parent = self.current_node
            self.current_node = self.current_node.left
        else :
            self.parent = self.current_node
            self.current_node = self.current_node.right
    if searched == False :
        return False

Case 1 : 삭제할 Node가 Leaf Node인 경우

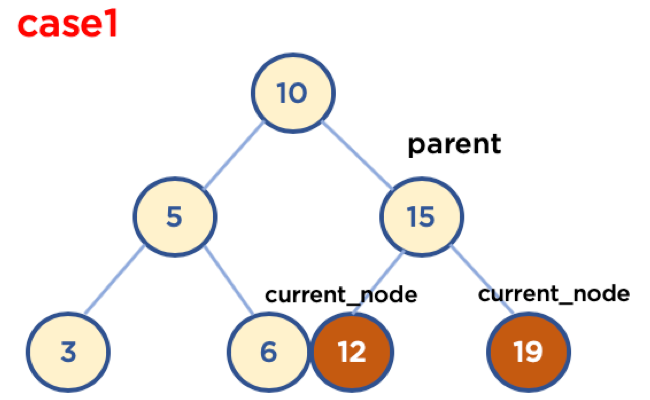
# self.current_node가 삭제할 Node, self.parent는 삭제할 Node의 Parent Node인 상태
if self.current_node.left == None and self.current_node.right == None :
    if value < self.parent.value :
        self.parent.left == None
    else :
        self.parent.right == None
    del self.current_node

Case 2 : 삭제할 Node가 Child Node를 한 개 가지고 있을 경우

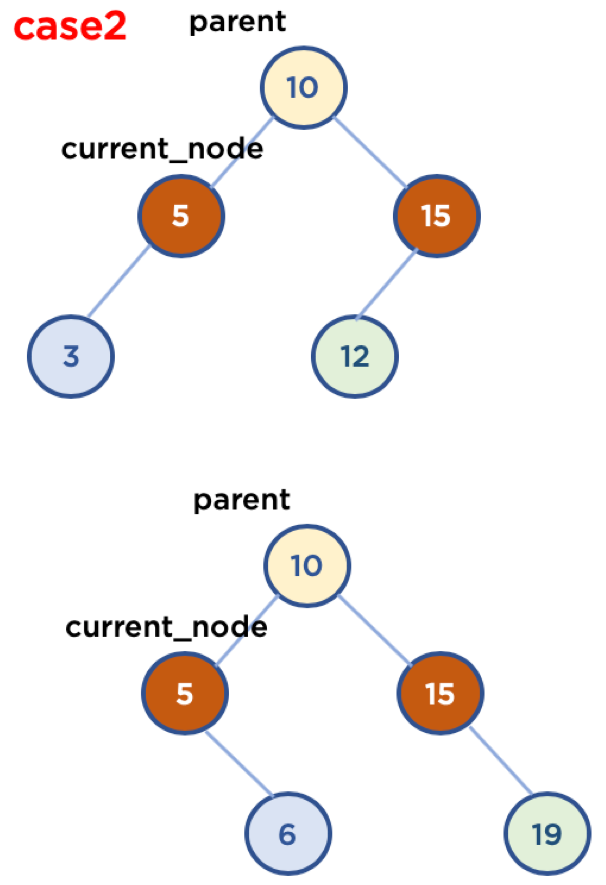
if self.current_node.left != None and self.current_node.right == None :
    if value < self.parent.value :
        self.parent.left = self.current_node.left
    else :
        self.parent.right = self.current_node.right
elif self.current_node.left == None and self.current_node.right != None :
    if value < self.parent.value :
        self.parent.left = self.current_node.right
    else :
        self.parent.right = self.current_node.right

Case 3-1 : 삭제할 Node가 Child Node를 두 개 가지고 있을 경우 (삭제할 Node가 Parent Node 왼쪽에 있을 때)
기본 사용 가능 전략
1. 삭제할 Node의 오른쪽 자식 중, 가장 작은 값을 삭제할 Node의 Parent Node가 가리키도록 함
2. 삭제할 Node의 왼쪽 자식 중, 가장 큰 값을 삭제할 Node의 Parent Node가 가리키도록 함
기본 사용 가능 전략 중, 1번 전략을 사용하여 코드를 구현
- Case3-1-1: 삭제할 Node가 Parent Node의 왼쪽에 있고, 삭제할 Node의 오른쪽 자식 중, 가장 작은 값을 가진 Node의 Child Node가 없을 때
- Case3-1-2: 삭제할 Node가 Parent Node의 왼쪽에 있고, 삭제할 Node의 오른쪽 자식 중, 가장 작은 값을 가진 Node의 오른쪽에 Child Node가 있을 때
  - 가장 작은 값을 가진 Node의 Child Node가 왼쪽에 있을 경우는 없음, 왜냐하면 왼쪽 Node가 있다는 것은 해당 Node보다 더 작은 값을 가진 Node가 있다는 뜻이기 때문

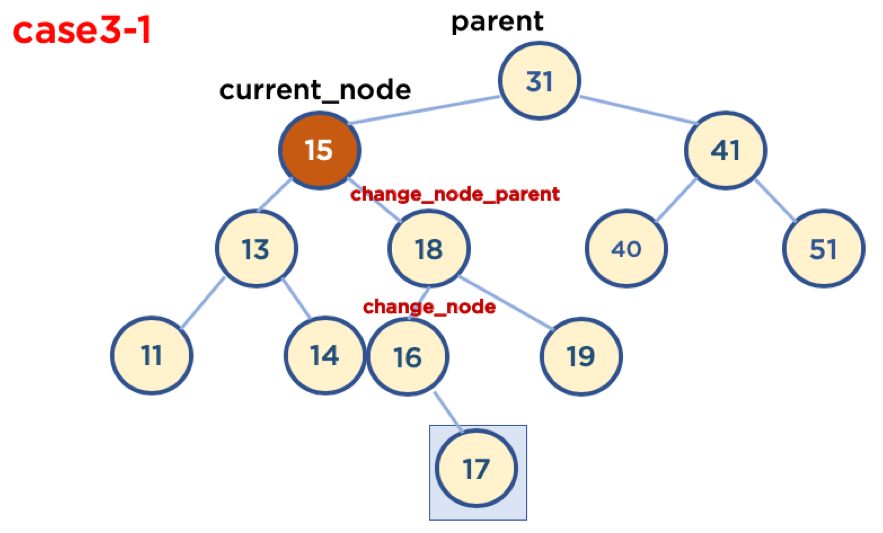
# case 3
if self.current_node.left != None and self.current_node.right != None :
    # case 3-1
    if value < self.parent.value :
        self.change_node = self.current_node.right
        self.change_node_parent = self.current_node.right
        while self.change_node.left != None :
            self.change_node_parent = self.change_node
            self.change_node = self.change_node.left
        if self.change_node.right != None :
            self.change_node_parent.left = self.change_node.right
        else :
            self.change_node_parent.left = None
        self.parent.left = self.change_node
        self.change_node.right = self.current_node.right
        self.change_node.left = self.change_node.left

Case 3-2 : 삭제할 Node가 Child Node를 두 개 가지고 있을 경우 (삭제할 Node가 Parent Node 오른쪽에 있을 때)
기본 사용 가능 전략
1. 삭제할 Node의 오른쪽 자식 중, 가장 작은 값을 삭제할 Node의 Parent Node가 가리키도록 함
2. 삭제할 Node의 왼쪽 자식 중, 가장 큰 값을 삭제할 Node의 Parent Node가 가리키도록 함
기본 사용 가능 전략 중, 1번 전략을 사용하여 코드를 구현
- Case3-2-1: 삭제할 Node가 Parent Node의 오른쪽에 있고, 삭제할 Node의 오른쪽 자식 중, 가장 작은 값을 가진 Node의 Child Node가 없을 때
- Case3-2-2: 삭제할 Node가 Parent Node의 오른쪽에 있고, 삭제할 Node의 오른쪽 자식 중, 가장 작은 값을 가진 Node의 오른쪽에 Child Node가 있을 때
  - 가장 작은 값을 가진 Node의 Child Node가 왼쪽에 있을 경우는 없음, 왜냐하면 왼쪽 Node가 있다는 것은 해당 Node보다 더 작은 값을 가진 Node가 있다는 뜻이기 때문

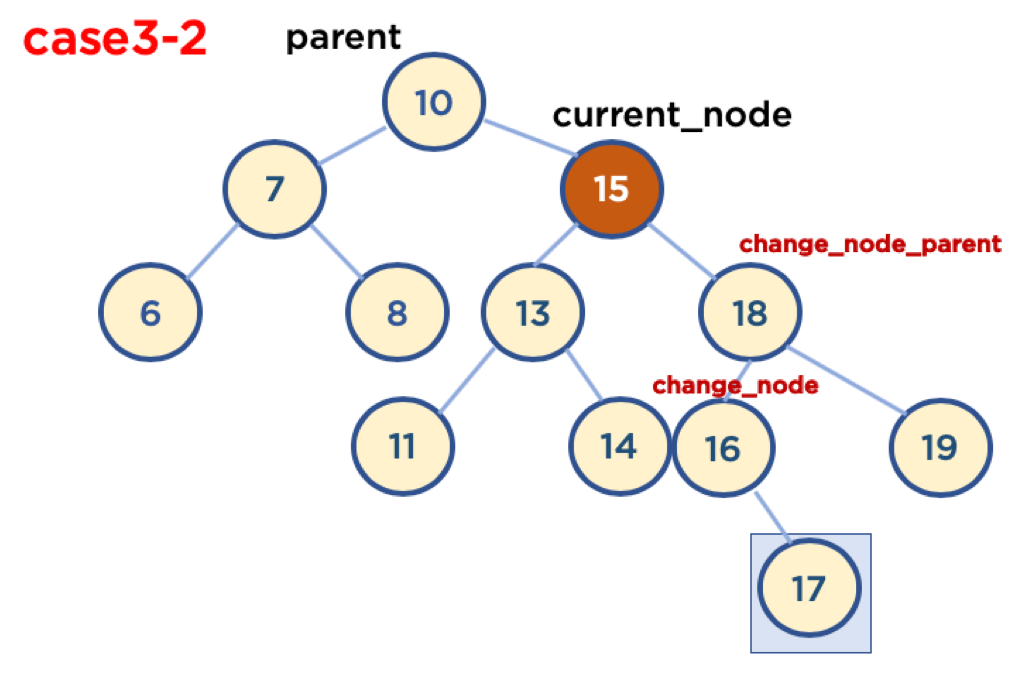
# case 3-2
else :
    self.change_node = self.current_node.right
    self.change_node_parent = self.current_node.right
    while self.change_node.left != None :
        self.change_node_parent = self.change_node
        self.change_node = self.change_node.left
    if self.change_node.right != None :
        self.change_node_parent.left = self.change_node.right
    else :
        self.change_node_parent.left = None
    self.parent.right = self.change_node
    self.change_node.left = self.current_node.left
    self.change_node.right = self.current_node.right

파이썬 전체 코드 구현

class Node :
    def __init__(self, value) :
        self.value = value
        self.left = None
        self.right = None

class NodeMgmt :
    def __init__(self, head) :
        self.head = head

    def insert(self, value) :
        self.current_node = self.head
        while True :
            if value < self.current_node.value :
                if self.current_node.left != None :
                    self.current_node = self.current_node.left
                else :
                    self.current_node.left = Node(value)
                    break
            else :
                if self.current_node.right != None :
                    self.current_node = self.current_node.right
                else :
                    self.current_node.right = Node(value)
                    break

    def search(self, value) :
        self.current_node = self.head
        while self.current_node :
            if self.current_node.value == value :
                return True
            elif value < self.current_node.value :
                self.current_node = self.current_node.left
            else :
                self.current_node = self.current_node.right
        return False

    def delete(self, value) :
        # 삭제할 노드 탐색
        searched = False
        self.current_node = self.head
        self.parent = self.head
        while self.current_node :
            if self.current_node.value == value :
                searched = True
                break
            elif value < self.current_node.value :
                self.parent = self.current_node
                self.current_node = self.current_node.left
            else :
                self.parent = self.current_node
                self.current_node = self.current_node.right
        if searched == False :
            return False
        # case 1
        if self.current_node.left == None and self.current_node.right == None :
            if value < self.parent.value :
                self.parent.left = None
            else :
                self.parent.right = None
        # case 2
        elif self.current_node.left != None and self.current_node.right == None :
            if value < self.parent.value :
                self.parent.left = self.current_node.left
            else :
                self.parent.right = self.current_node.left
        elif self.current_node.left == None and self.current_node.right != None :
            if value < self.parent.value :
                self.parent.left = self.current_node.right
            else :
                self.parent.right = self.current_node.right
        # case 3
        elif self.current_node.left != None and self.current_node.right != None :
            # case 3-1
            if value < self.parent.value :
                self.change_node = self.current_node.right
                self.change_node_parent = self.current_node.right
                while self.change_node.left != None :
                    self.change_node_parent = self.change_node
                    self.change_node = self.change_node.left
                if self.change_node.right != None :
                    self.change_node_parent.left = self.change_node.right
                else :
                    self.change_node_parent.left = None
                self.parent.left = self.change_node
                self.change_node.right = self.current_node.right
                self.change_node.left = self.change_node.left
            # case 3-2
            else :
                self.chagne_node = self.current_node.right
                self.change_node_parent = self.current_node.right
                while self.change_node.left != None :
                    self.change_node_parent = self.change_node
                    self.change_node = self.change_node.left
                if self.change_node.right != None :
                    self.change_node_parent.left = self.change_node.right
                else :
                    self.change_node_parent.left = None
                self.parent.right = self.change_node
                self.change_node.right = self.current_node.right
                self.change_node.left = self.current_node.left
        return True

참고 : http://ejklike.github.io/2018/01/09/traversing-a-binary-tree-1.html
파이썬 전체 코드 테스트
- random 라이브러리 활용
- random.randint(첫번째 숫자, 마지막 숫자): 첫번째 숫자부터 마지막 숫자 사이에 있는 숫자를 랜덤하게 선택해서 리턴
- 예: random.randint(0, 99): 0에서 99까지 숫자중 특정 숫자를 랜덤하게 선택해서 리턴해줌

# 0 ~ 999 숫자 중에서 임의로 100개를 추출해서, 이진 탐색 트리에 입력, 검색, 삭제
import random

# 0 ~ 999 중, 100 개의 숫자 랜덤 선택
bst_nums = set()
while len(bst_nums) != 100 :
    bst_nums.add(random.randint(0, 999))

# print(bst_nums)

# 선택된 100개의 숫자를 이진 탐색 트리에 입력, 임의로 루트노드는 500을 넣기로 함
head = Node(500)
binary_tree = NodeMgmt(head)
for num in bst_nums :
    binary_tree.insert(num)

# 입력한 100개의 숫자 검색 (검색 기능 확인)
for num in bst_nums :
    if binary_tree.search(num) == False :
        print("search failed", num)

# 입력한 100개의 숫자 중 10개의 숫자를 랜덤 선택
delete_nums = set()
bst_nums = list(bst_nums)
while len(delete_nums) != 10 :
    delete_nums.add(bst_nums[random.randint(0, 99)])

# 선택한 10개의 숫자를 삭제 (삭제 기능 확인)
for del_num in delete_nums :
    if binary_tree.delete(del_num) == False :
        print("delete failed", del_num)

- 이진 탐색 트리의 시간 복잡도와 단점

@1. 시간 복잡도 (탐색시)

depth (트리의 높이) 를 h라고 표기한다면, O(h)
n개의 노드를 가진다면, $h = log_2{n} $ 에 가까우므로, 시간 복잡도는 $ O(log{n}) $
- 참고: 빅오 표기법에서 $log{n}$ 에서의 log의 밑은 10이 아니라, 2
- 한번 실행시마다, 50%의 실행할 수도 있는 명령을 제거한다는 의미. 즉 50%의 실행시간을 단축시킬 수 있다는 것을 의미

(출처: https://www.mathwarehouse.com/programming/gifs/binary-search-tree.php#binary-search-tree-insertion-node)

@2. 이진 탐색 트리 단점

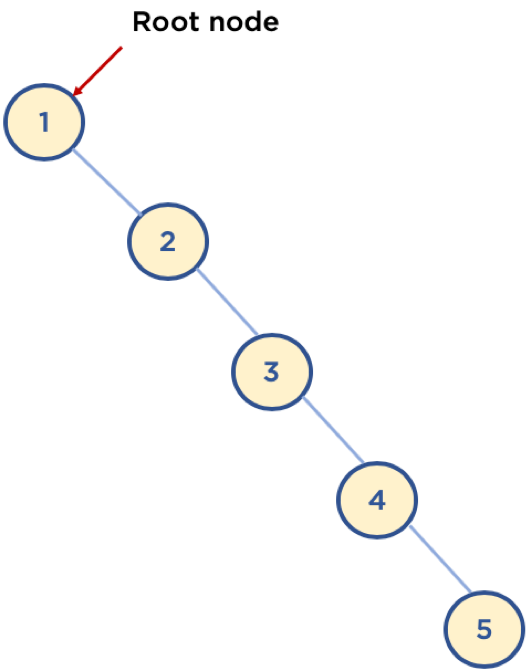
평균 시간 복잡도는 $ O(log{n}) $ 이지만, 이는 트리가 균형잡혀 있을 때의 평균 시간복잡도
최악의 경우는 링크드 리스트등과 동일한 성능을 보여줌 ( $O(n)$ )

Twitter Facebook LinkedIn

LWW

[Data Structure] 트리(Tree)

1. 트리

- 트리 (Tree) 구조

- 알아둘 용어

- 이진 트리와 이진 탐색 트리

- 자료 구조 이진 탐색 트리의 장점과 주요 용도

- 이진트리와 정렬된 배열간의 탐색 비교

- 파이썬으로 이진 탐색 트리 구현하기

@1. 노드 클래스 만들기

@2. 이진 탐색 트리에 데이터 넣기

@3. 이진 탐색 트리 탐색

@4. 이진 탐색 트리 삭제

@5. 이진 탐색 트리 삭제 코드 구현과 분석

- 이진 탐색 트리의 시간 복잡도와 단점

@1. 시간 복잡도 (탐색시)

@2. 이진 탐색 트리 단점

공유하기

댓글남기기

참고

[Baekjoon] 9076번 : 점수 집계

[Baekjoon] 5545번 : 최고의 피자

[Baekjoon] 20540번 : 연길이의 이상형

[Baekjoon] 4811번 : 알약