[Algorithm] 삽입 정렬(Insertion Sort)

1. 삽입 정렬 (Insertion Sort)

- 삽입 정렬이란?

• 삽입 정렬은 두 번째 인덱스부터 시작
• 해당 인덱스(key 값) 앞에 있는 데이터(B)부터 비교해서 key 값이 더 작으면, B값을 뒤 인덱스로 복사
• 이를 key 값이 더 큰 데이터를 만날때까지 반복, 그리고 큰 데이터를 만난 위치 바로 뒤에 key 값을 이동
• 직접 눈으로 보기 : https://visualgo.net/en/sorting

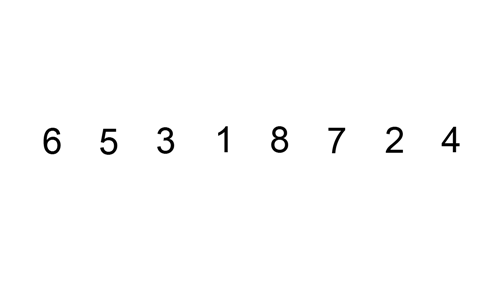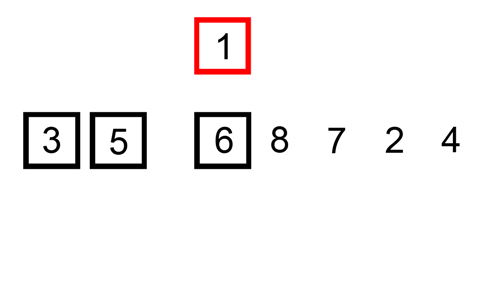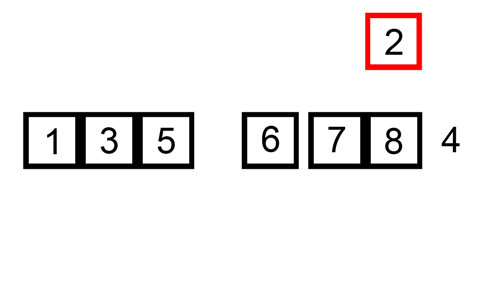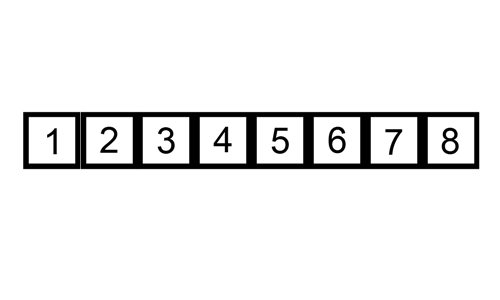
출처: https://commons.wikimedia.org/wiki/File:Insertion-sort-example.gif

- 어떻게 코드로 만들까?

• 데이터가 네 개 일때 : data_list = [9, 3, 2, 5]
  • 처음 한번 실행하면, key값은 9, 인덱스(0) - 1 은 0보다 작으므로 끝 : [9, 3, 2, 5]
  • 두 번째 실행하면, key값은 3, 9보다 3이 작으므로 자리 바꾸고, 끝 : [3, 9, 2, 5]
  • 세 번째 실행하면, key값은 2, 9보다 2가 작으므로 자리 바꾸고, 다시 3보다 2가 작으므로 끝 : [2, 3, 9, 5]
  • 네 번째 실행하면, key값은 5, 9보다 5이 작으므로 자리 바꾸고, 3보다는 5가 크므로 끝 : [2, 3, 5, 9]

2. 알고리즘 구현

1. for stand in range(len(data_list)) 로 반복
2. key = data_list[stand]
3. for num in range(stand, 0, -1) 반복
   • 내부 반복문 안에서 data_list[stand] < data_list[num - 1] 이면,
     • data_list[num - 1], data_list[num] = data_list[num], data_list[num - 1]

def insertion_sort(data) :
  for i in range(len(data) - 1) :
    for j in range(i + 1, 0, -1) :
      if data[j] < data[j - 1] :
        data[j], data[j - 1] = data[j - 1], data[j]
      else :
        break
  return data


# 테스트
import random

data_list = random.sample(range(100), 10)
print(insertion_sort(data_list))  # [13, 40, 58, 64, 79, 86, 92, 94, 95, 99]

3. 알고리즘 분석

• 반복문이 두 개 O($n^2$)
• 최악의 경우, $\frac { n * (n - 1)}{ 2 }$
• 완전 정렬이 되어 있는 상태라면 최선은 O(n)

참고 코드 : https://goo.gl/XKBXuk